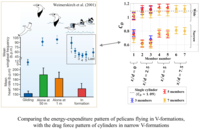
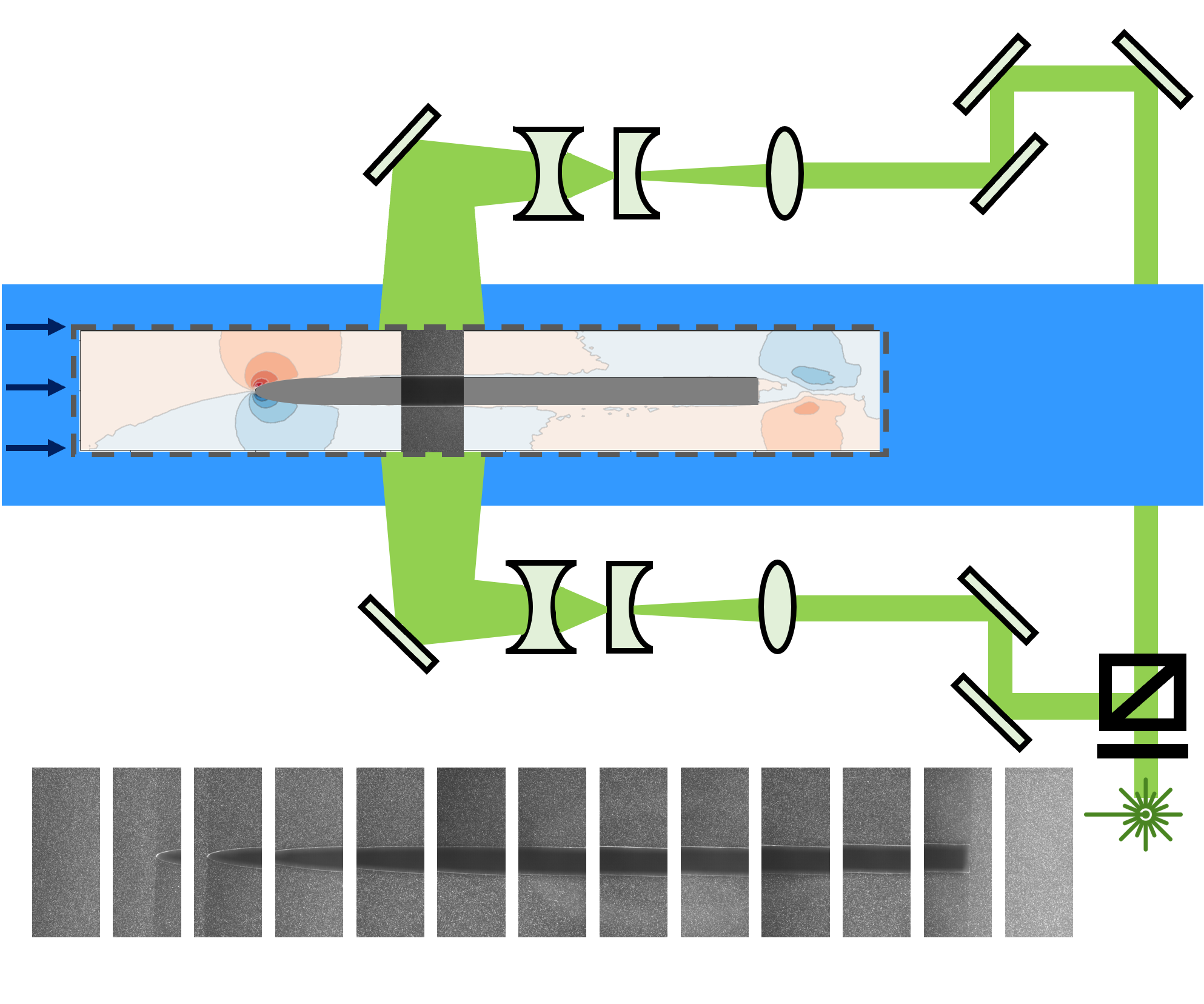
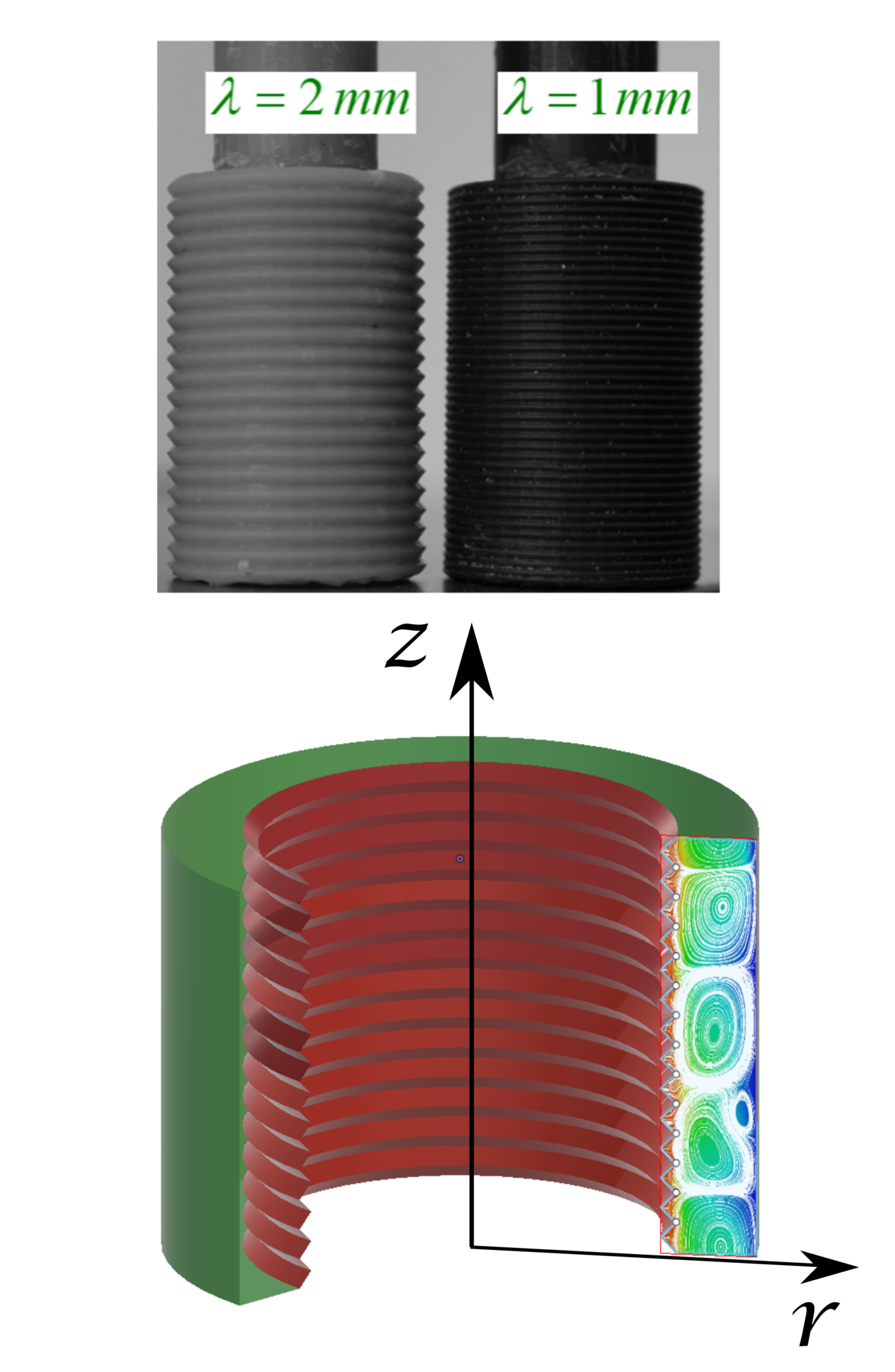
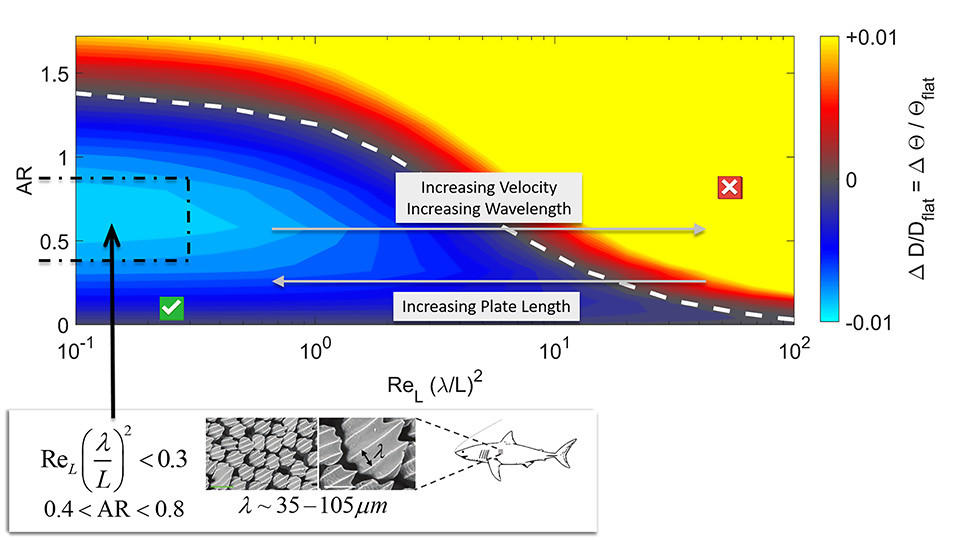
Shabnam Raayai-Ardakani and Tal Cohen. 9/2019. “
Capturing Strain Stiffening Using Volume Controlled Cavity Expansion.” Extreme Mechanics Letters, 31, Pp. 100536.
Publisher's Version Shabnam-Raayai Ardakani and Gareth H. McKinley. 5/2/2019. “
Geometric optimization of riblet-textured surfaces for drag reduction in laminar boundary layer flows.” Physics of Fluids, 31, 5, Pp. 053601.
Publisher's VersionAbstractMicro-scale riblets are shown to systematically modify viscous skin friction in laminar flows at high Reynolds numbers. The textured denticles of native sharkskin are widely cited as a natural example of this passive drag reduction mechanism. Since the structure of a viscous boundary layer evolves along the plate, the local frictional drag changes are known empirically to be a function of the length of the plate in the flow direction, as well as the riblet spacing, and the ratio of the height to spacing of the riblets. Here, we aim to establish a canonical theory for high Reynolds number laminar flow over V-groove riblets to explore the self-similarity of the velocity profiles and the evolution of the total frictional drag exerted on plates of different lengths. Scaling analysis, conformal mapping, and numerical calculations are combined to show that the potential drag reduction achieved using riblet surfaces depends on an appropriately rescaled form of the Reynolds number and on the aspect ratio of the riblets (defined in terms of the ratio of the height to spacing of the texture). We show that riblet surfaces require a scaled Reynolds number lower than a maximum threshold to be drag-reducing and that the change in drag is a nonmonotonic function of the aspect ratio of the riblet texture. This physical scaling and the computational results presented here can be used to explain the underlying physical mechanism of this mode of passive drag reduction to rationalize the geometric dimensions of shark denticles, as well as the results of experiments with shark denticle replicas of various sizes, and guide designs for optimizing the textural parameters that result in friction-reducing surfaces.
Shabnam Raayai-Ardakani, Darla Earl, and Tal Cohen. 5/2019. “
The Intimate Relationship between Cavitation and Fracture.” Soft Matter, 15, 255, Pp. 4999-5005.
Publisher's VersionAbstractNearly three decades ago, the field of mechanics was cautioned of the obscure nature of cavitation processes in soft materials [A. Gent, Cavitation in rubber: a cautionary tale, Rubber Chem. Technol., 1990, 63, 49–53]. Since then, the debate on the mechanisms that drive this failure process is ongoing. Using a high precision volume controlled cavity expansion procedure, this paper reveals the intimate relationship between cavitation and fracture. Combining a Griffith inspired formulation for crack propagation, and a Gent inspired formulation for cavity expansion, we show that despite the apparent complexity of the fracture patterns, the pressure–volume response follows a predictable path. In contrast to available studies, both the model and our experiments are able to track the entire process including the unstable branch, by controlling the volume of the cavity. Moreover, this minimal theoretical framework is able to explain the ambiguity in previous experiments by revealing the presence of metastable states that can lead to first order transitions at onset of fracture. The agreement between the simple theory and all of the experimental results conducted in PDMS samples with shear moduli in the range of 25–246 [kPa] confirms that cavitation and fracture work together in driving the expansion process. Through this study we also determine the fracture energy of PDMS and show its significant dependence on strain stiffening.